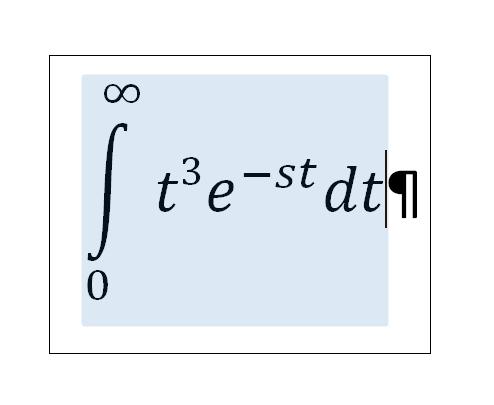Thread Starter
- Mitglied seit
- 04.05.2001
- Beiträge
- 10.850
Probleme bei den Hausaufgaben ?
Tipp : Gemeinsam nach der Schule mit einem Kaffee erledigen, Schulbücher sind eine tolle Erfindung, im Unterricht aufpassen auch Dann gibt es noch Google, Google ist allwissend. Wenn´s doch mal nicht reicht, dürfen in diesem Thread Fragen gestellt werden und Antworten gegeben werden. Gerne auch mit einer Tasse Kaffee neben der Tastatur...
Dann gibt es noch Google, Google ist allwissend. Wenn´s doch mal nicht reicht, dürfen in diesem Thread Fragen gestellt werden und Antworten gegeben werden. Gerne auch mit einer Tasse Kaffee neben der Tastatur...
Grüße
Dennis
Tipp : Gemeinsam nach der Schule mit einem Kaffee erledigen, Schulbücher sind eine tolle Erfindung, im Unterricht aufpassen auch
Grüße
Dennis